IOI2009 raisins 题解

Edited on | In | Comments:

Problem

问题描述：

普罗夫迪夫的著名巧克力大师Bonny需要切开一板带有葡萄干的巧克力。巧克力是一个包含许多相同的方形小块的矩形。小块沿着巧克力的边排列成$n$行$m$列，即共有$n×m$块。每个小块上有$1$个或多个葡萄干，没有葡萄干在小块的边上或者跨过两个小块。

最开始，巧克力是一整块。Bonny需要把它切成上述的$n×m$个独立的小块。因为Bonny很忙，她需要她的助手Sly Peter帮她切。Peter只能从一端到另一端切直线并且他要为他的每一刀得到报酬。Bonny手头没有钱，但是她有足够的葡萄干，所以她提出用葡萄干付给Peter。Sly Peter同意接受葡萄干，但是有下面的条件：每次他把给定的一块巧克力切成两小块，他都要得到和那块给定的巧克力上葡萄干数目相同的葡萄干。

Bonny想要付给Peter尽可能少的葡萄干。她知道这$n×m$个小块中每一个小块上葡萄干的数目。她可以选择递给Peter的巧克力的顺序，也可以告诉Peter如何切(横切还是竖切)以及从哪里切。请告诉Bonny如何把巧克力切成一个个独立的小块。使她能够付给Sly Peter尽可能少的葡萄干。

任务

写一个程序，给定每个小块上葡萄干的数目，计算Bonny要付给Sly Peter的最少的葡萄干的数目。

数据规模

$1≤n,m≤50$ 巧克力两条边上小块的数目

$1≤R_{k,p}≤1,000$ 第$k$行第$p$列的小块上的葡萄干数目

有25分的评测数据，$n,m≤7$。

输入

你的程序必须从标准输入中读取下列数据：

第一行包含整数$n$和$m$，以一个空格隔开。

接下来的n行描述了每个小块上葡萄干的数目。这n行中第$k$行描述的是第$k$行小块巧克力。每行包含$m$个整数，分别以一个空格隔开。这些整数描述的是该行从左到右的小块。第$k$行的第$p$个整数表示位于第$k$行第$p$列的小块上的葡萄干数目。

输出

你的程序必须向标准输出写入一行，该行包含一个整数Bonny：要付给Sly Peter的最少的葡萄干的数目。

样例

1
2
3
4
Input #1
2 3
2 7 5
1 9 5
1
2
Output #1
77

img

img

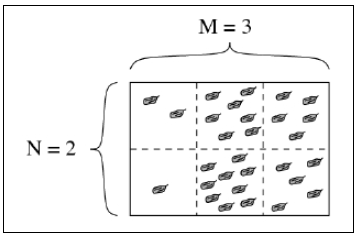
一种可能的花费$77$的切法(许多种之一)：

第一刀，将第$3$列切下，Bonny要付给Peter$29$个葡萄干。

接下来，Bonny将小的一块给Peter：两小块各有$5$个葡萄干的那块，Peter把它从中切开得到$10$个葡萄干。

接下来，Bonny给Peter第一刀后较大的一块：有$2,7,1$和$9$个葡萄干的那块，Bonny要求Peter横切，即将第一和第二行分开，得到$19$个葡萄干。

接下来，Bonny要求Peter切开左上部的一块，付$9$个葡萄干。最后，Bonny要求Peter切开左下部的一块，付$10$个葡萄干。

Bonny的总花费是$29+10+19+9+10=77$个葡萄干。没有其他的切法能够花费更少的葡萄干而把该巧克力切成$6$小块。

Solution

二分错解

我最先的睿智想法：既然越少越好，那么

——–以下是扯淡内容，读者请不要相信——–

左右两边越平均越好（不知道哪里来的稀奇想法）

——–以下不是扯淡内容——–

对于这种题，显然做一个前缀和。

又因为$1≤n,m≤50$，则可以做$4$维前缀和，把每一个可能割出来的巧克力块上的葡萄干数全部记录下来（有的是空间）。

接下来进行分治，根据我的稀奇想法，二分前缀和找到平衡线使割开的两部分上的葡萄干数尽量接近。

接下来就是递归啊递归啊递归啊递归…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#include <bits/stdc++.h>
using namespace std;

const int MAXN = 50 + 5;
int n, m;
long long raisin[MAXN][MAXN];
long long sum[MAXN][MAXN], cnt[MAXN][MAXN][MAXN][MAXN];
long long ans;

long long area(int ldx, int ldy, int urx, int ury)
{
    return sum[urx][ury] - sum[ldx - 1][ury]
        - sum[urx][ldy - 1] + sum[ldx - 1][ldy - 1];
}

long long dfs(int ldx, int ldy, int urx, int ury, bool k) //k表示横向切还是纵向切
{
    int l, r;
    long long ans1 = LONG_LONG_MAX, ans2 = LONG_LONG_MAX;
    double half = cnt[ldx][ldy][urx][ury] / 2.0; //当前处理的巧克力上葡萄干总数的一半，不用double也行
    if (k)
    {
        //二分思想：左右两边最接近，即左边和总数一半接近，二分刀切在哪里
        l = ldx, r = urx;
        while (l + 1 < r)
        {
            int mid = (l + r) / 2;
            if (cnt[ldx][ldy][mid][ury] > half) r = mid;
            else l = mid;
        }
        //选l和r中离总数一半最接近的切
        int flag = (fabs(half - cnt[ldx][ldy][l][ury]) < fabs(cnt[ldx][ldy][r][ury] - half) ? l : r);
        if (flag == ldx && ldy == ury) ans1 = cnt[ldx][ldy][ldx][ldy]; //切下来边长为1
        else
        {
            if (flag != ldx) ans1 = dfs(ldx, ldy, flag, ury, 1);  //长>1，可以切
            if (ldy != ury)    ans1 = min(ans1, dfs(ldx, ldy, flag, ury, 0)); //宽>1，可以切
        }
        if (flag + 1 == urx && ldy == ury) ans2 = cnt[urx][ury][urx][ury];
        else
        {
            if (flag + 1 != urx) ans2 = dfs(flag + 1, ldy, urx, ury, 1);
            if (ldy != ury) ans2 = min(ans2, dfs(flag + 1, ldy, urx, ury, 0));
        }
        return ans1 + ans2 + cnt[ldx][ldy][urx][ury];
    }
    else
    {
        l = ldy, r = ury;
        while (l + 1 < r)
        {
            int mid = (l + r) / 2;
            if (cnt[ldx][ldy][urx][mid] > half) r = mid;
            else l = mid;
        }
        int flag = (fabs(half - cnt[ldx][ldy][urx][l]) < fabs(cnt[ldx][ldy][urx][r] - half) ? l : r);
        if (flag == ldy && ldx == urx) ans1 = cnt[ldx][ldy][ldx][ldy];
        else
        {
            if (flag != ldy) ans1 = dfs(ldx, ldy, urx, flag, 0);
            if (ldx != urx) ans1 = min(ans1, dfs(ldx, ldy, urx, flag, 1));
        }
        if (flag + 1 == ury && ldx == urx) ans2 = cnt[urx][ury][urx][ury];
        else
        {
            if (flag + 1 != ury) ans2 = dfs(ldx, flag + 1, urx, ury, 0);
            if (ldx != urx) ans2 = min(ans2, dfs(ldx, flag + 1, urx, ury, 1));
        }
        return ans1 + ans2 + cnt[ldx][ldy][urx][ury];
    }
}

int main()
{
    freopen("raisins.in", "r", stdin); freopen("raisins.sol", "w", stdout);
    cin >> n >> m;
    if (n == 1 && m == 1) { cin >> raisin[1][1]; cout << 0 << endl; return 0; }
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> raisin[i][j];
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            sum[i][j] = sum[i - 1][j] + sum[i][j - 1]
            - sum[i - 1][j - 1] + raisin[n - j + 1][i];
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= i; k++)
                for (int l = 1; l <= j; l++)
                    cnt[k][l][i][j] = area(k, l, i, j);
    if (n != 1) ans = dfs(1, 1, m, n, 0);
    if (m != 1) ans = min(ans, dfs(1, 1, m, n, 1));
    cout << ans - cnt[1][1][m][n] << endl;
    return 0;
}

完美地WA了。

找了两天bug没找出来，只好否认：自己的算法错了。

于是一时性起：

不用二分了，我倒要看看暴力能拿几分！

正解

正解就是暴力。

把上面一段代码的二分部分改成

1
for (int flag = ldx; flag < urx; flag++)

就能TLE。（手动滑稽

空间多到溢出的我又开始挥霍：记忆化每一个巧克力块的最小切割支出。

然而还是TLE了。

又想了半天优化，突然发现，之前是因为不能把边长为1的线段进行二分才加了那么多判断的，现在可是暴力啊，循环条件直接给舍了边长为1的情况了，于是愉快地把特判给省了。

然后就能发现，$k=true$或$k=false$是一样的情况，舍了。

就这么AC了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>
using namespace std;

const int MAXN = 50 + 5;
int n, m;
int raisin[MAXN][MAXN];
int sum[MAXN][MAXN], cnt[MAXN][MAXN][MAXN][MAXN];
int memory[MAXN][MAXN][MAXN][MAXN];  //记忆化
int ans = INT_MAX;

int dfs(int ldx, int ldy, int urx, int ury)
{
    if (memory[ldx][ldy][urx][ury]) return memory[ldx][ldy][urx][ury]; //记忆化
    if (ldx == urx && ldy == ury) return cnt[ldx][ldy][urx][ury]; //边长为1
    int pay, tot = INT_MAX;
    for (int flag = ldx; flag < urx; flag++) //横向切
    {
        pay = dfs(ldx, ldy, flag, ury) + dfs(flag + 1, ldy, urx, ury);
        if (tot > pay) tot = pay;
    }
    for (int flag = ldy; flag < ury; flag++) //纵向切
    {
        pay = dfs(ldx, ldy, urx, flag) + dfs(ldx, flag + 1, urx, ury);
        if (tot > pay) tot = pay; //pay取最小值
    }
    memory[ldx][ldy][urx][ury] = tot + cnt[ldx][ldy][urx][ury];
    //返回：自己的花费+上一层自己一块所占的花费
    return memory[ldx][ldy][urx][ury];
}

int main()
{
    cin >> n >> m;
    //边长为1不用切，输出0
    if (n == 1 && m == 1) { cin >> raisin[1][1]; cout << 0 << endl; return 0; }
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> raisin[i][j];
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            sum[i][j] = sum[i - 1][j] + sum[i][j - 1]
            - sum[i - 1][j - 1] + raisin[n - j + 1][i];
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= i; k++)
                for (int l = 1; l <= j; l++)
                    cnt[k][l][i][j] = sum[i][j] - sum[k - 1][j]
                        - sum[i][l - 1] + sum[k - 1][l - 1];
    //以上前缀和
    ans = dfs(1, 1, m, n);
    cout << ans - cnt[1][1][m][n] << endl; //由于第一刀没有再上一层，减去总数
    return 0;
}

Data

测试数据 提取码：0q3s