BOI2010 grid 题解

Edited on | In | Comments:

Problem

题目描述

考虑下面的字母网格:

img

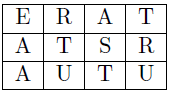
从字母网格读取的单词TARTU有7种方式:

img

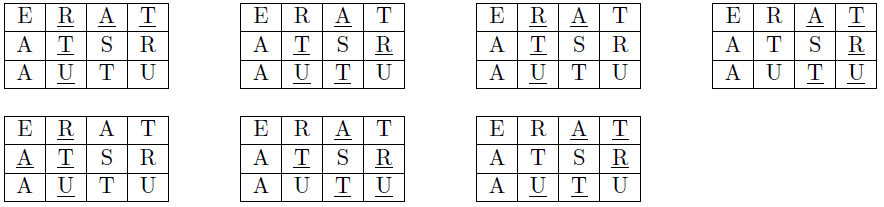
给出字母网格中的一个单词，请你计算从字母网格的读取这个单词的方式个数。单词的第一个字母，可以从字母网格的任意单元格开始，下一个字母可从相邻单元(水平,垂直或对角线)读取。读单词时，一个单元格字母可多次读取。

输入格式：

第一行包含三个整数：$H(H≤200)$网格的高度，$W(W≤200)$网格的宽度，和$L(L≤100)$单词的最大长度。

下面的$H$行，每行$W$个字母描述网格。最后一行是长度为$L$单词。网格和单词都是大写的英文字母(A~Z)。

输出格式：

仅输出一个整数，你可以假设方案个数不超过${10}^{18}$。

样例输入输出：

1
2
3
4
5
6
Input #1
3 4 5
ERAT
ATSR
AUTU
TARTU
1
2
Output #1
7
1
2
3
4
5
Input #2
2 2 10
AA
AA
AAAAAAAAAA
1
2
Output #2
78732

Solution

搜索

首先想到的自然是搜索。

于是最劣运算次数约为：$200×8^{99}≈5.1×10^{91}‬$

暴搜挂着机，打表出省一

对于深搜最常用的两种优化：剪枝、记忆化。

好像这道题不能剪枝？那就用记忆化。

$f[x][y][depth]$记录当前坐标上的字母为第$depth$位时之后有多少种可行方案。

迭代模拟

由于当前一层的地图（即$f[][][depth]$）只受上一层地图（即$f[][][depth-1]$）的影响，因此可以考虑将递归转迭代。

$f[x][y][depth]$记录当前坐标上的字母为第$depth$位时有多少种可行方案。

可以发现$f[x][y][depth]$就是它周围$8$个方格里的$f[][][depth-1]$之和。

特殊情况：

$letter[x][y]≠word[depth]$，则$f[x][y][depth]=0$;

$depth=1且letter[x][y]=word[depth]$，则$f[x][y][depth]=1$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <bits/stdc++.h>
using namespace std;

const int dx[8] = { 1, 1, 0, -1, -1, -1, 0, 1 };
const int dy[8] = { 0, 1, 1, 1, 0, -1, -1, -1 };
const int MAXN = 200 + 5;
const int MAXLEN = 100 + 5;
int n, m, len;
char _map[MAXN][MAXN], word[MAXLEN];
long long f[MAXLEN][MAXN][MAXN];
long long ans;

int main()
{
    cin >> n >> m >> len;
    for (int i = 1; i <= n; i++)
    {
        _map[i][0] = getchar();
        for (int j = 1; j <= m; j++) _map[i][j] = getchar();
    }
    word[0] = getchar();
    for (int i = 1; i <= len; i++) word[i] = getchar();
    for (int i = 1; i <= len; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= m; k++)
            {
                if (_map[j][k] != word[i]) { f[i][j][k] = 0; continue; }
                if (i == 1) { f[i][j][k] = 1; continue; }
                for (int diri = 0; diri < 8; diri++)
                    f[i][j][k] += f[i - 1][j + dx[diri]][k + dy[diri]];
            }
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            ans += f[len][i][j];
    cout << ans << endl;
    return 0;
}

当然写成滚动数组更好，但是本人太懒，外加数据范围不大，为了增加代码可读性，没有展示滚动数组的代码。

Data

链接：https://pan.baidu.com/s/1UUtmZlnT5NjhE_8nDr-Euw

提取码：grwc

数据仓库：https://github.com/Fanhy531/testdata